2. Развертки пирамидальных и конических поверхностей
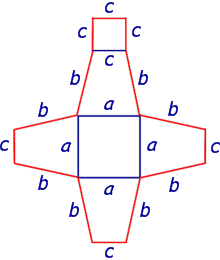
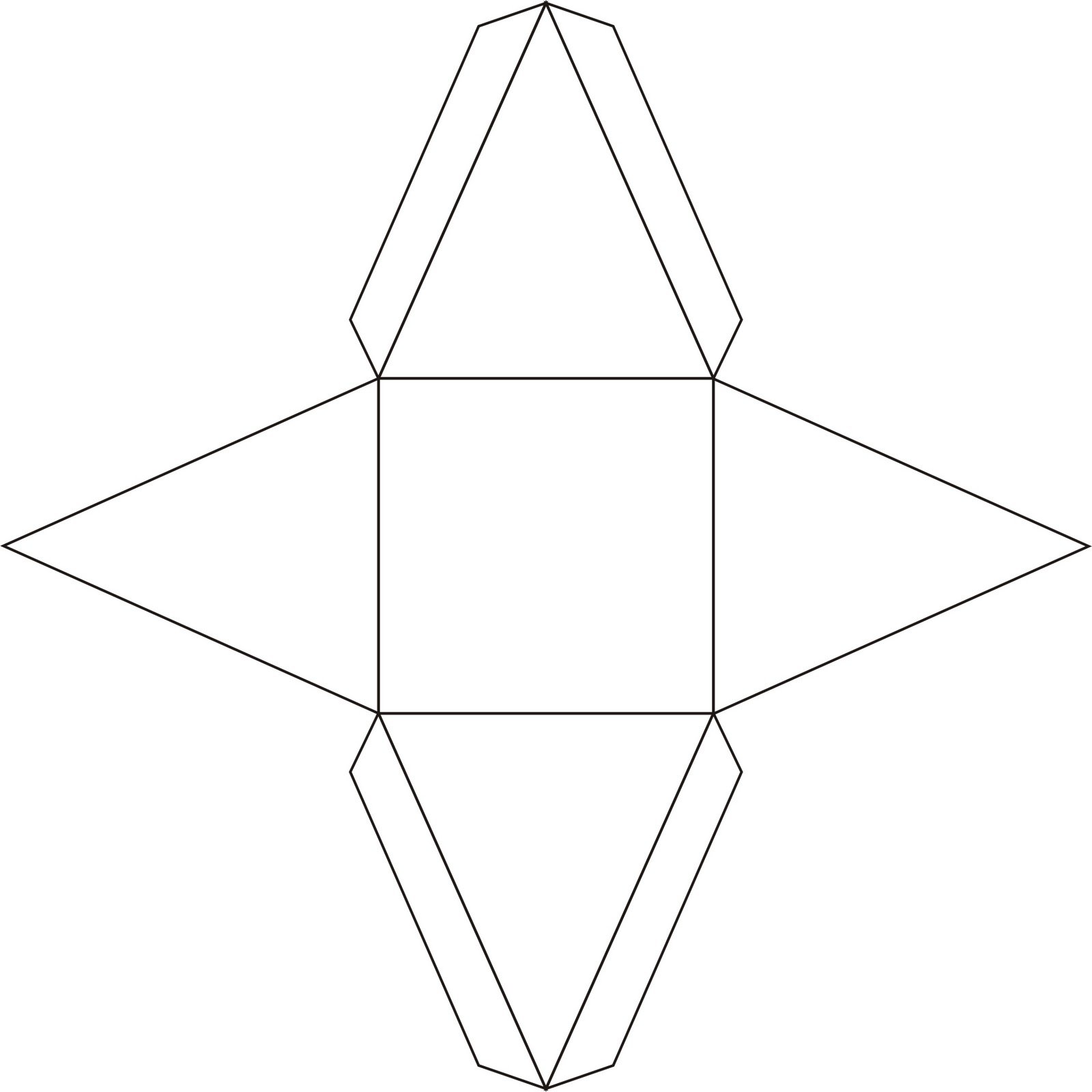
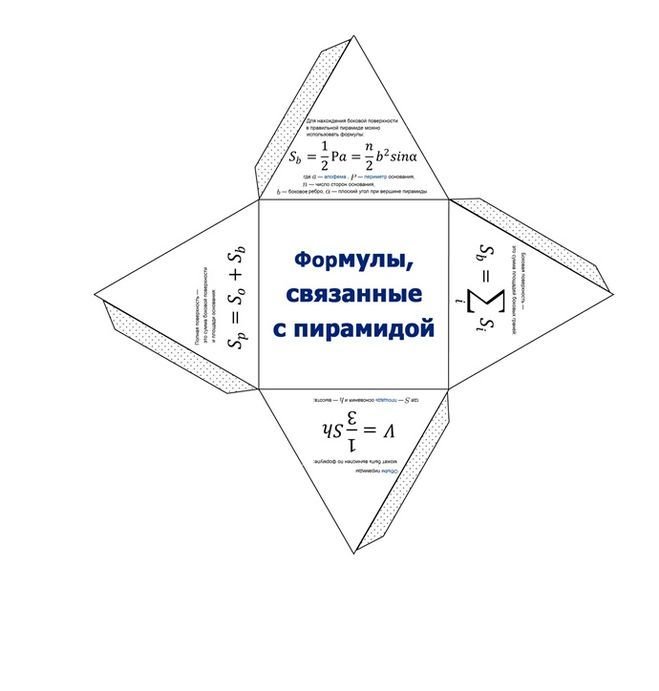
В основании пирамиды правильный четырехугольник - квадрат все стороны которого равны, углы между сторонами основания составляют 90 градусов. Высота пирамиды находится точно в центре четырехугольного основания. Скачать развертку правильной четырехугольной пирамиды для печати на листе А4 Все боковые грани пирамиды - правильные треугольники. Почтовые марки охватывают все значимые события в мире. Не обошли вниманием художники-филателисты и изображения многогранников.




Глава 11. Метрические задачи
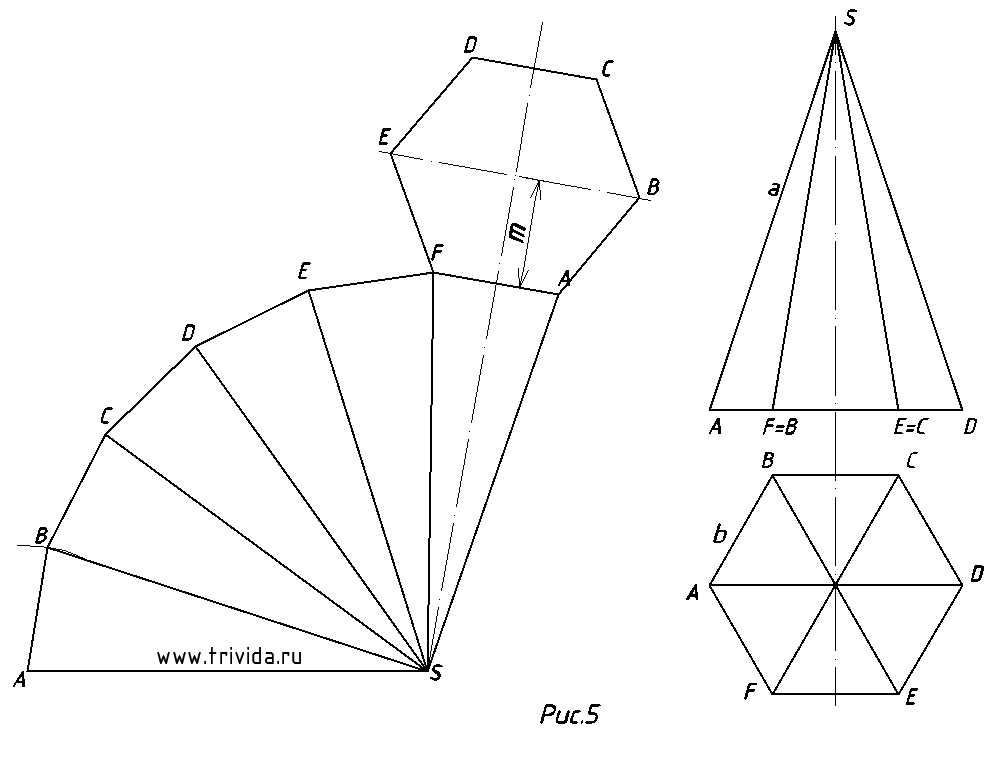
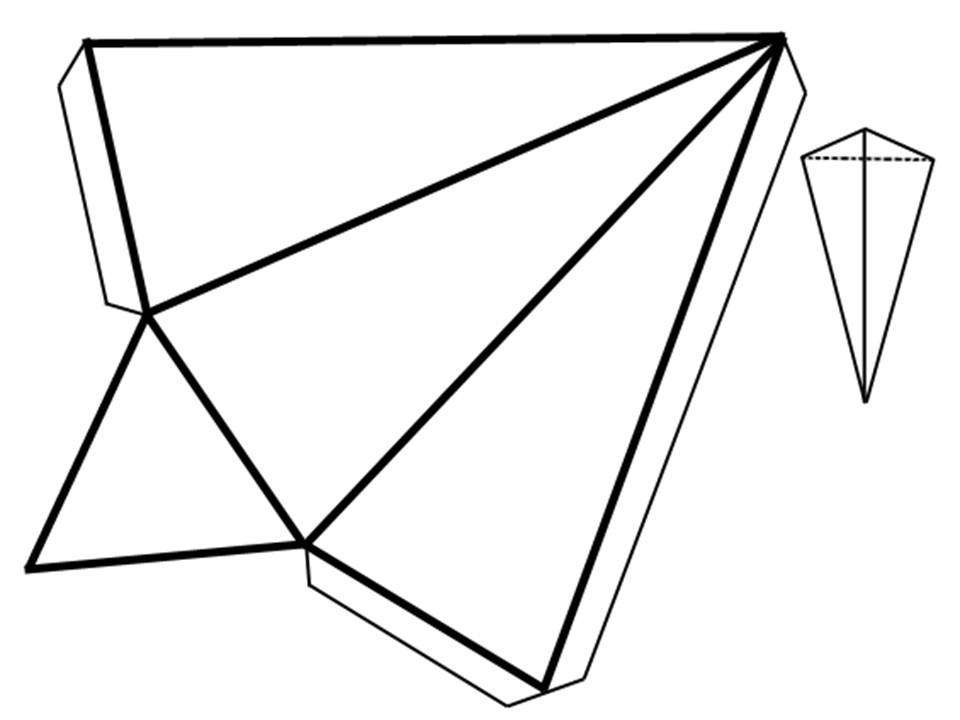
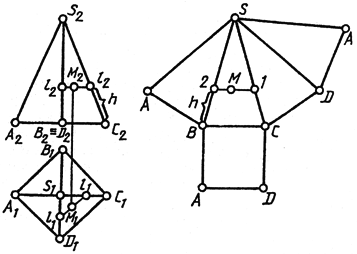
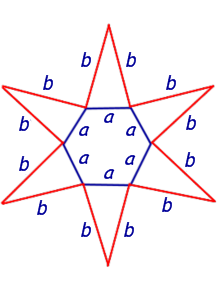
Развертка поверхности правильной пирамиды представляет собой плоскую фигуру, составленную из боковых граней - равнобедренных или равносторонних треугольников и правильного многоугольника основания. Для примера взята правильная четырехугольная пирамида. Из произвольной точки S0, как из центра, проводят дугу окружности радиуса L, равного длине бокового ребра пирамиды, так как в данном примере ребра пирамиды являются линиями уровня. По этой дуге откладывают четыре отрезка, равных стороне основания пирамиды, которое на ортогональном чертеже спроецировано в натуральную величину, так как тоже является линией уровня.





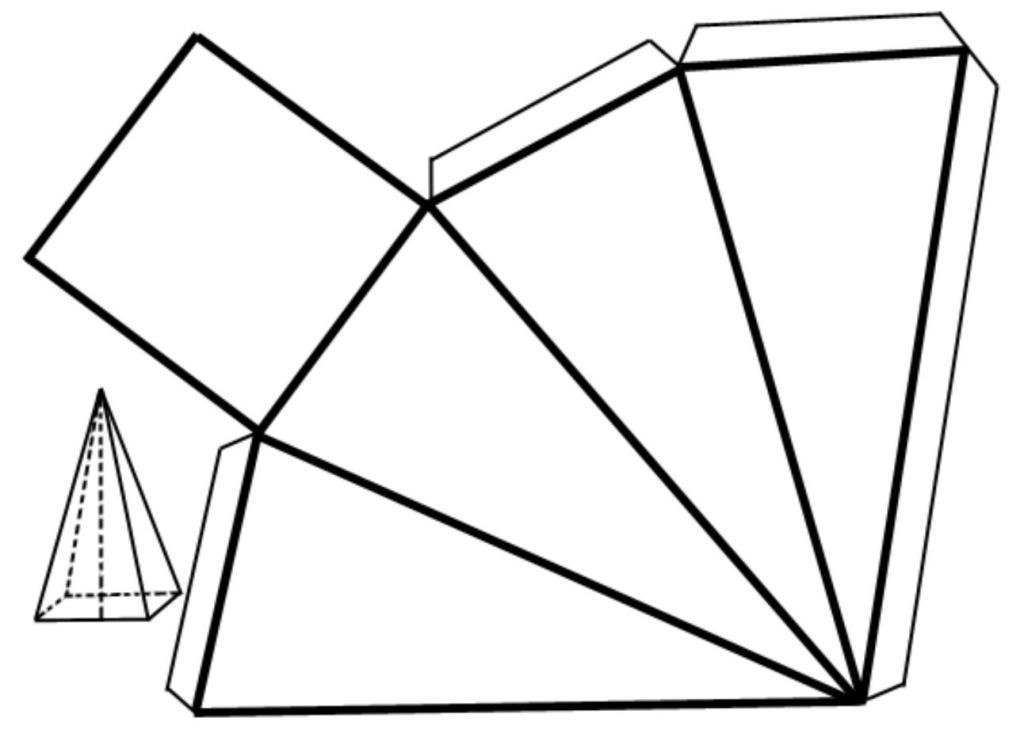
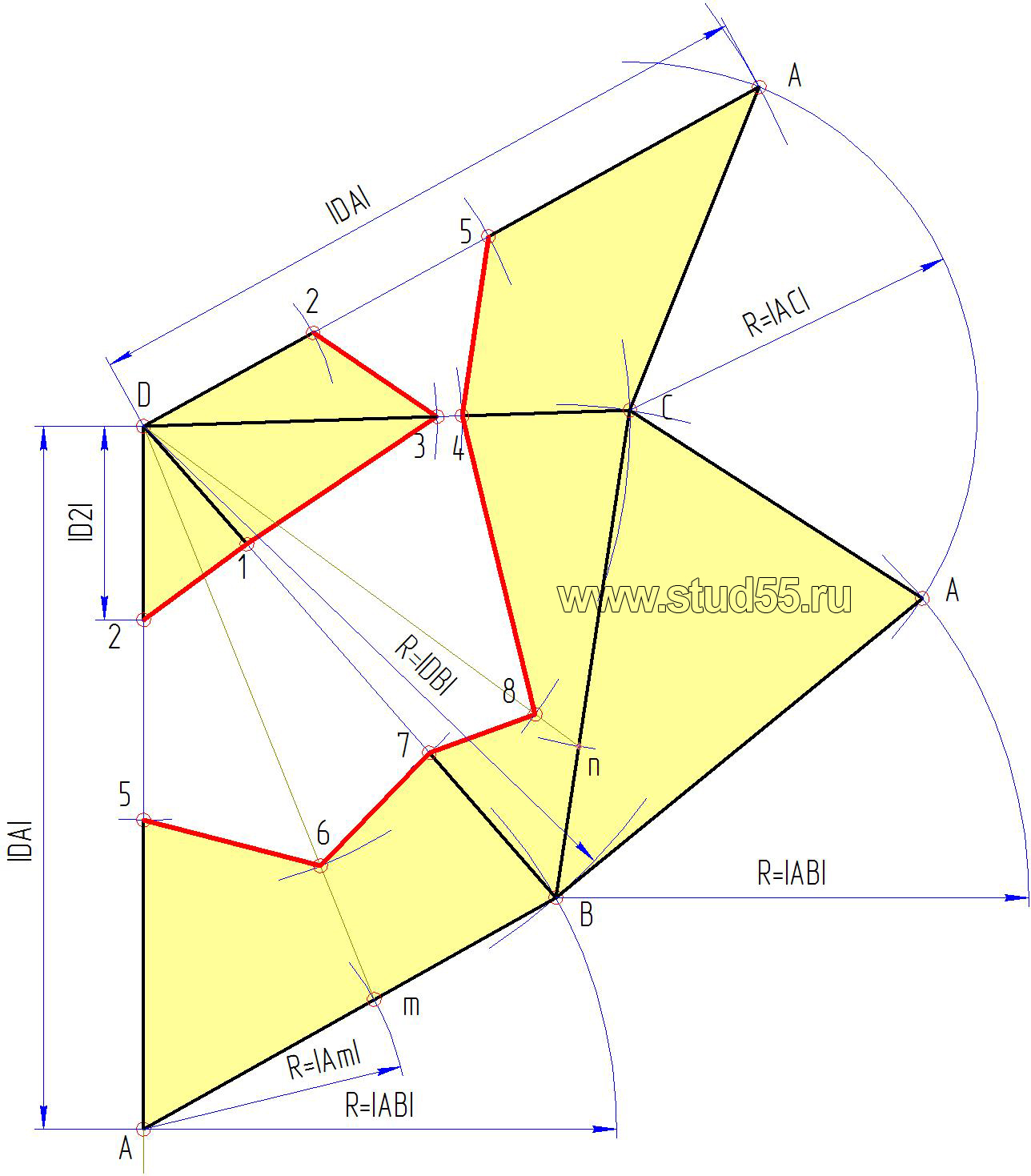



| 157 | Необходимо построить развертки гранных тел и нанесения на развертку линии пересечения призмы и пирамиды. | |
| 386 | Некоторые предметы упаковочные коробки, канцелярские папки, водосточные трубы и др. Для их изготовления пользуются развёртками. | |
| 358 | Разделы: Начальная школа. | |
| 166 | Развертка 4-х гранной пирамиды. |
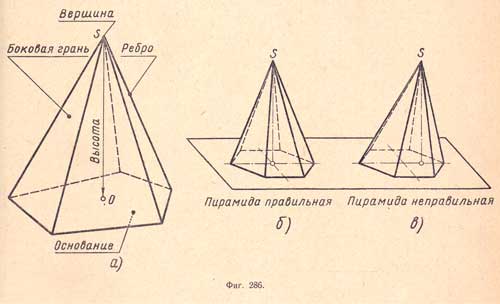
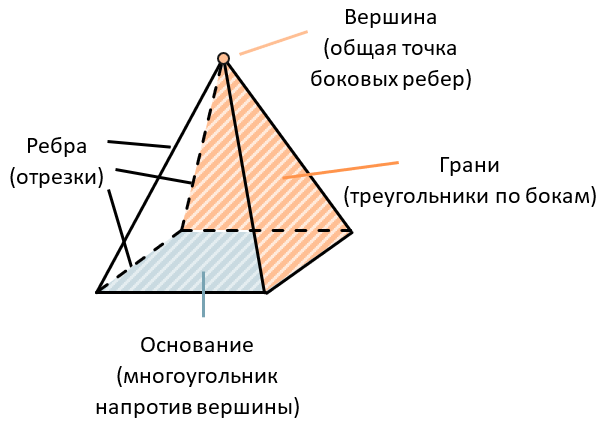
Отправить комментарий. Развертка пирамиды. Пирамида - это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции.